 |
Addition
|
 |
Subtraction
|
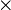 or or  |
Multiplication
|
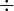 or or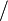 |
Division
|
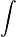 |
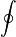 |
integration is over a closed surface
|
|
 |
Therefore, so. hence
|
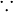 |
Because, Since
|
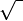 |
Square root
|
$\sqrt[4]{5}$
|
|
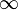 |
Infinity
|
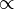 |
Proportion
|
 |
is equal to
|
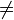 |
is not equal to
|
 |
approximately equal
|
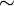 |
is similar to
|
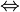 |
if and only if
|
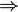 |
implies; if ... then
|
 |
is less than
|
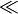 |
is much less than
|
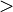 |
is greater than
|
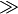 |
is much greater then
|
 |
is less than or equal to
|
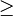 |
is greater than or equal to
|
 |
sub set
|
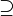 |
super set
|
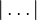 |
absolute value of; modulus of
|
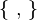 |
the set of ...
|
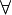 |
for all
|
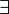 |
there exist
|
 |
is an element of;
|
 |
is not an element of
|
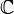 |
Complex number
|
 |
Natural number
|
 |
Real number
|
Integer
|
|
Rational number
|
Irrational number
|
||
Very useful, essential and interesting subject, if we can understand and use it properly, otherwise not.
Tuesday, October 20, 2015
Mathematical Symbol
Labels:
Insert
Subscribe to:
Post Comments (Atom)

No comments:
Post a Comment