Function
In mathematics, a function is a
relation between a set of inputs and a set of permissible outputs
with the property that each input is related to exactly one output.
Example:
Let f(x)=x2
be a function, if the input is −3, then the output is 9, and we may
write f(−3) = 9. Likewise, if the input is 3, then the output is
also 9, and we may write f(3) = 9.
Undefined
A function is said to be "undefined" at points not in its domain. For example, in the real number system,
is undefined for negative 
, i.e., no such values exist for function 
.
The set of numbers for which a function is defined is called the domain of the function. If a number is not in the domain of a function, the function is said to be "undefined" for that number. Two common examples are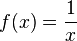
, which is undefined for 
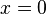, and , which is undefined (in the real number system) for negative .
Limit
limit is the value that a function or sequence "approaches" as the input or index approaches some value.Limits are used to define continuity, derivatives and integrals.
Indeterminate form
If the expression obtained after this substitution does not give enough information to determine the original limit, it is said to take on an indeterminate form.
The indeterminate forms typically considered in the literature are denoted 0/0, ∞/∞, 0 × ∞, ∞ − ∞, 00, 1∞ and ∞0.
Undefined
A function is said to be "undefined" at points not in its domain. For example, in the real number system,
is undefined for negative , i.e., no such values exist for function .The set of numbers for which a function is defined is called the domain of the function. If a number is not in the domain of a function, the function is said to be "undefined" for that number. Two common examples are
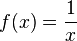, which is undefined for 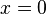, and , which is undefined (in the real number system) for negative .Limit
limit is the value that a function or sequence "approaches" as the input or index approaches some value.Limits are used to define continuity, derivatives and integrals.
Indeterminate form
If the expression obtained after this substitution does not give enough information to determine the original limit, it is said to take on an indeterminate form.
The indeterminate forms typically considered in the literature are denoted 0/0, ∞/∞, 0 × ∞, ∞ − ∞, 00, 1∞ and ∞0.
No comments:
Post a Comment